Coordinate systems in Map Viewer and TerraFlex
An advantage of using TerraFlex to update your GIS, is that the Map Viewer, TerraFlex, and the configurable real time correction sources for collecting data for your project all use the same coordinate system settings. Any data you add to the map workspace must be in either the same datum as that used by the map workspace, or you can import files that are in the WGS 1984 datum.
Because all data in the project is in the same coordinate system, this reduces a major source of error common to GIS workflows, where feature data must transit through one or more systems or applications and use a different coordinate system in each application. When comparing coordinates of newly collected GIS features with previously collected feature data with different coordinate system-related properties, errors are frequently seen. For example, failing to properly handle differences in GNSS and GIS coordinate systems in North America can cause a GIS feature “offset” of up to 1.5 m.
Several concepts are key to understanding the impact of coordinate systems and geodetics on GIS data collection workflows.
When performing any sort of measurement, it is necessary to have some point of origin (or “zero” point) against which the measurement is made. To compare two or more measurements and determine the difference, you need to use the same point of origin. For example, when describing the height of a wall between two properties, you need to convey from what side of the wall the measurement was made. Measuring positions on the Earth is no exception, although it is made more complicated by the Earth’s irregular shape. In geodetics, the surface of the Earth is approximated by an ellipsoid. Locations, or geodetic coordinates, on this ellipsoid can then be described in terms of latitude (relative to the equator), longitude (relative to the Prime Meridian), and height (above the ellipsoid). The particular ellipsoid used to model the shape of the Earth, its center of mass, and the system used to define lines of latitude and longitude on this ellipsoid, is known as a geodetic datum, or simply datum.

Datums are commonly categorized as global versus local. As the name implies, a global datum is applicable to the entire surface of the Earth and typically fixed to the center of the Earth. Global datums are used by GNSS systems. There are two major global datum “standards” - the World Geodetic System (WGS) driven by the U.S. Department of Defense and the International Terrestrial Reference Frame (ITRF) driven by the International Earth Rotation and Reference Systems Service. In both cases, there are periodic datum updates or realizations with increased accuracy due to use of better (more accurate and more recent) measurements of the Earth and its continual changes. The most recent realizations of ITRF and WGS can be regarded as identical for the same point in time.
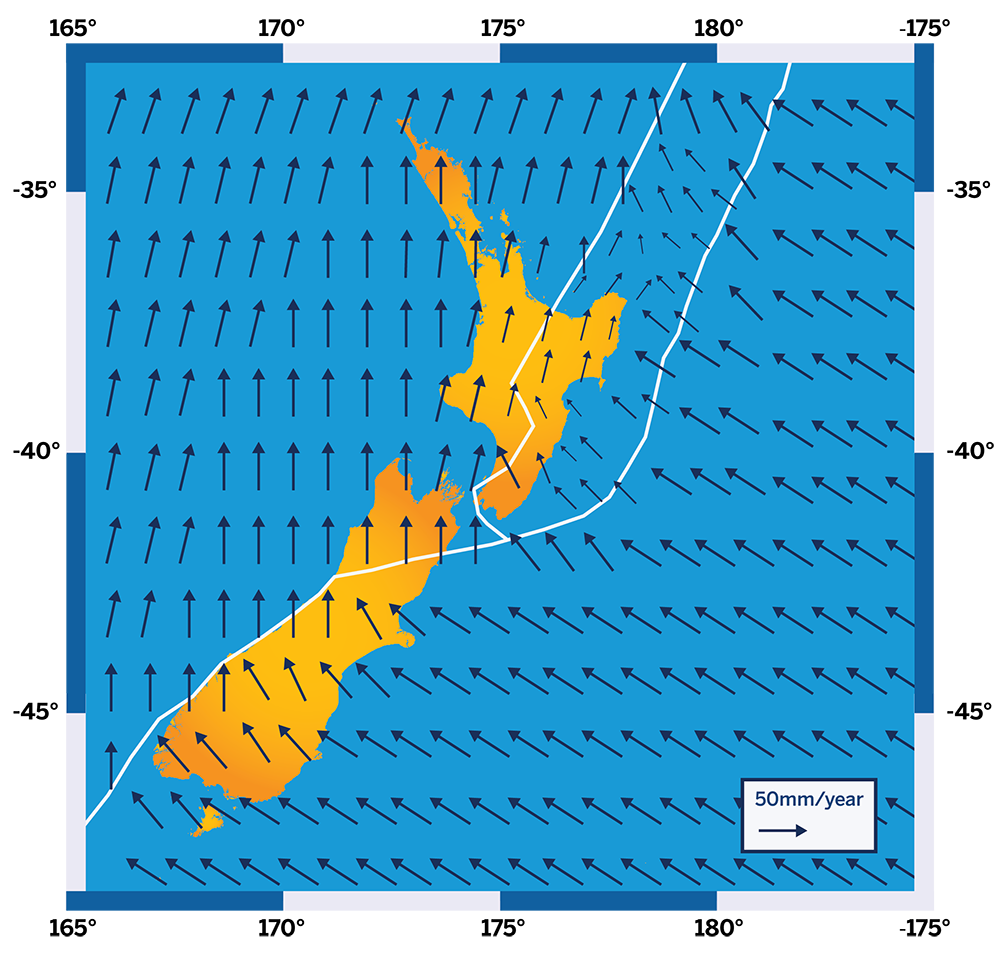
The primary challenge with using a global datum like ITRF2014 or WGS84 as the frame of reference for your GIS data is that global coordinates used to represent the features you have mapped will change over time. All objects on the Earth’s surface (for example, trees, roads, pipes) move together with the tectonic plates on which they are located. Each plate is moving relative to the Earth’s center where global datums are generally fixed, and the movement of each plate is in a different speed (about 10 cm/year on average), direction, and rate of rotation. That means the ITRF2014 coordinate of an object mapped today, will have a different ITRF2014 coordinate if you come back after 5, 10, or 20 years and map that same object again, because the tectonic plate you are standing on will have drifted to a different location over time, perhaps as far as tens of centimeters!
A common way to avoid the challenges with global datums is through the use of local datums instead. As the name implies, local datums are best used in a local area where the datum can be fixed to one or more physical objects or locations on the Earth’s surface (for example, a single tectonic plate) where everything is moving at the same speed and direction. Coordinates are relative to these reference objects or locations. Local datums work well for areas with uniform tectonic motion (such as Australia).
Another way of categorizing datums is by how they change – or don’t change – over time. This is referred to as static versus dynamic. When referenced to a static datum, coordinates representing the locations of features do not change over time. This is typical when a local datum is fixed to a single tectonic plate and the movement of that plate is uniform. Static datums can still be adjusted over time through new realizations. Examples of static datums are GDA94 in Australia and ETRS89 in Europe.
Alternatively, the use of dynamic datums is for handling the case where coordinates are changing constantly because of non-uniform tectonic movement (such as crustal deformation or earthquakes). By their nature, all global datums are dynamic due to constant tectonic motion; coordinates of surface features will be constantly changing as the reference point of the global datum is fixed to the center of the Earth, and not any particular point on it. As a special case, semi-dynamic datums allow for changes in coordinates at discrete moments in time, typically following large earthquakes. The NZGD2000 datum in New Zealand is an example of a semi-dynamic datum. The most important factor with dynamic and semi-dynamic datums is that coordinates must take into account the time when the coordinate, or feature, was calculated or collected (X, Y, Z, t). In geodesy, this reference to time of a measurement is called an epoch.
An epoch is a moment in time used as a reference point for some time-varying measurement. For example, when measuring the flow of a river, the reporting of the measurement will almost always include an element of time (the river was flowing at 30 cubic meters per second at 10AM on the 10th of January in 2006), otherwise the measurement holds much less value (how to compare it historically?). This is also true for geodetic coordinates measured against dynamic datums. Because the coordinates of surface features are constantly changing, it is very important that the measurement include the time at which the measurement was made.
In geodesy, an epoch is usually expressed as a decimal number showing a year (the integer part) and part of the year (the decimal part). For example, we might refer to coordinates “as of 2020.00” which means, coordinates “as of January 1, 2020”. When fully describing a datum (which can also be dynamic, remember), the datum ‘tag’ will typically include the epoch, along with the realization, for proper naming and identification. For example, the proper name of the latest horizontal datum used in the United States is “NAD 1983 (2011) Epoch 2010.00.” This reinforces the fact that the reference epoch of NAD 1983 (2011) is indeed 2010.00.
The combination of datum + epoch is often referred to as the reference frame.
When working with GIS data, and in particular GIS data collected through GNSS collection methods, it is likely that you will need to convert data between datums. The most basic example of this is taking the GNSS positions that use a global datum and storing them as features in your GIS using a local datum. As mentioned above, the same position on the Earth will often have different coordinates between those two datums. We accomplish this through datum transformations.
A datum transformation is a mathematical formula, with parameters, for converting coordinates from one datum to another. There are various types of datum transformations, and they all generally accomplish this same purpose. A simple example would be a 3-parameter Molodensky transformation to indicate a shift in X, Y, and Z axes along with the differences in ellipsoids (simplified shape of the Earth) used between the two datums. A more precise computation involves 7 parameters: the 3 offsets plus 3 rotation parameters plus a scale parameter. Generally, when performing a datum transformation involving a dynamic datum, a specific epoch is assumed (typically the reference epoch). For areas with surface deformation, a grid-based transformation may be used. These transformations, and specifically the parameters for them, are developed by the scientific community and/or government agencies, and are available in Trimble Geospatial software.
To properly handle transformations involving dynamic datums with different epochs (specifically, non-reference epochs), time-dependent datum transformations must be used for optimal results. These transformations take into account models of tectonic plate movement (such as MORVEL and NNR-MORVEL56), which can often be modeled accurately unless they are close to plate boundaries. When using time-dependent transformations – typically 14 parameter – coordinate conversion between different epochs are reasonably accurate in areas with uniform tectonic motion. These have a historical use in scientific applications, and increasing use in survey applications; however, these are not yet widely available in GIS applications.
Regions like New Zealand, California and Japan are hard to model using standard tools, due to the extensive surface deformation caused by multi-directional surface movement at different velocities (typical at plate boundaries). In these cases, manual tools provided by government agencies include additional elements such as the modeling of crustal deformation (for example, NGS HTDP) for the most accurate results.
Incorrect handling of datum transformations can be a major source of error in GIS data collection projects. Specifically, in decreasing order of magnitude of the error:
-
Failing to set a proper datum. For example, the difference between NAD83 and WGS84/ITRF08 is up to 1.5 m.
-
Selecting the wrong datum transformation. For example, selecting a null datum transformation when coordinate transformation is actually required.
-
Not taking time into account when converting from dynamic datums – up to 7 cm/year.
-
Accuracy of published transformations, which is based on the underlying models.
-
Numeric errors of transformation functions.
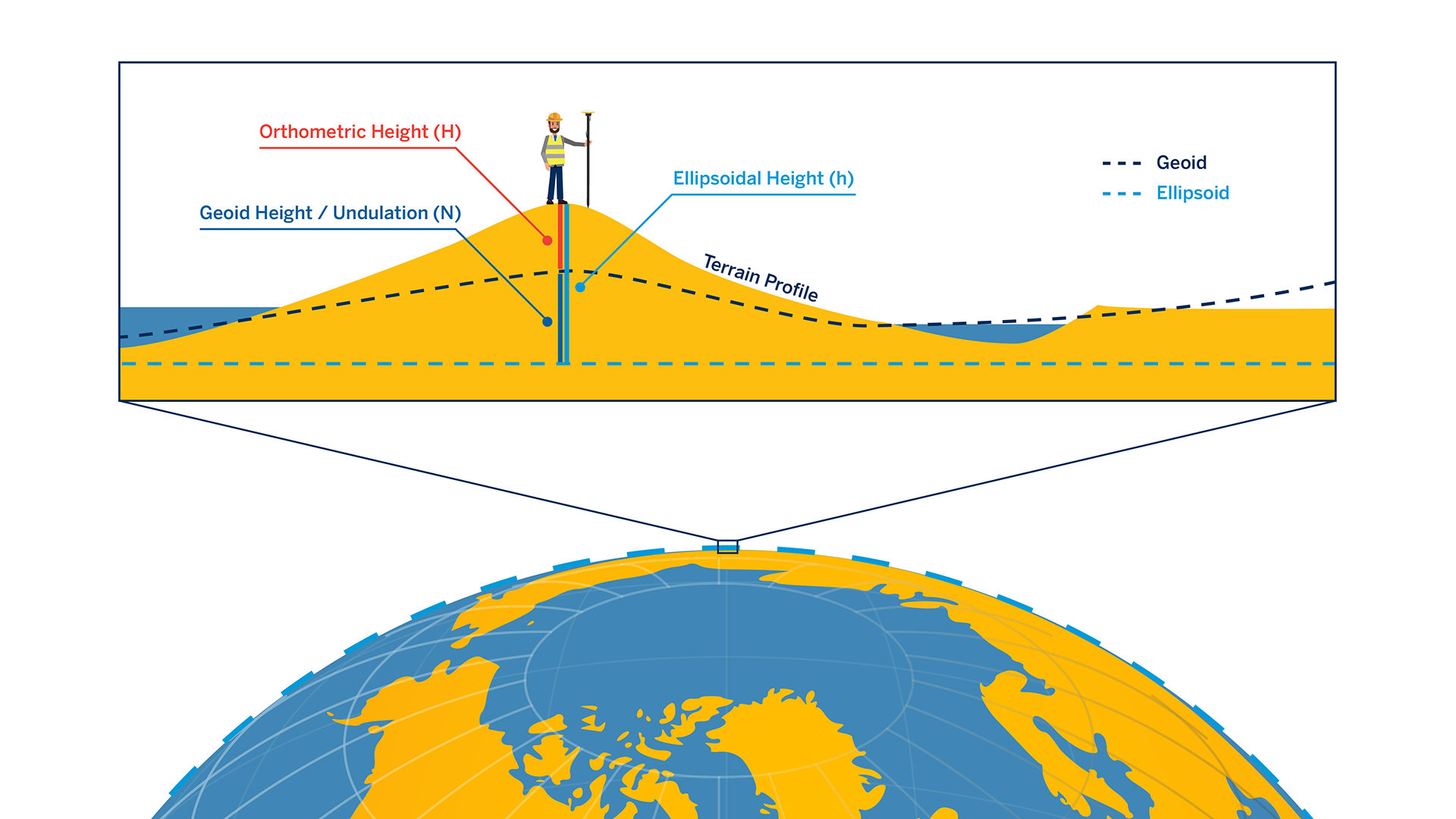
To compare measured elevations or heights, it is necessary to use a common vertical reference, or datum. Perhaps the most common vertical datum in use by GIS professionals is that of mean sea level or MSL. Heights relative to mean sea level are more generally called orthometric heights. The challenge with GNSS data collection is that by default, all GNSS coordinate measurements and calculations assume results relative to the WGS84 ellipsoid only, which is explicitly not mean sea level. These native heights from the GNSS receiver are typically called height above ellipsoid or HAE. To calculate orthometric height, a proper geoid correction must be applied, where a geoid is a model of global mean sea level relative to a selected ellipsoid (model of the Earth). When converting between different datums, the heights above the ellipsoids must be adjusted if the datums use different ellipsoids.
A map projection is a way to represent (flatten) the 3D surface of the Earth on a 2D plane for cartography or display. All map projections distort the surface in some fashion, and no single projection is best for all purposes or in all regions. In general, the map projection selected is chosen because it preserves at least one property from area, shape, direction, bearing, distance and/or scale. When performing a map projection, geographic coordinates (latitude/longitude) are turned into Cartesian, or polar, plane coordinates (y/x or northing/easting).
More information on coordinate systems, and the common pitfalls associated with working with GIS data is covered in our blog series Coordinate Systems in Trimble GIS Workflows.